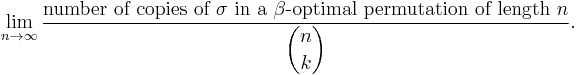Permutation pattern

In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. The permutation π, written as a word in one-line notation (i.e., in two-line notation with the first line omitted), is said to contain the permutation σ if there exists a subsequence of entries of π that has the same relative order as σ, and in this case σ is said to be a pattern of π, written σ ≤ π. Otherwise, π is said to avoid the permutation σ. The subsequence of π need not consist of consecutive entries. For example, permutation π = 391867452 (written in one-line notation) contains the pattern σ = 51342, as can be seen by considering the subsequence 91672. Such a subsequence is called a copy or instance of σ.

Contents

Prehistory

A case can be made that Percy MacMahon was the first to prove a result in the field with his study of "lattice permutations" in Volume I, Section III, Chapter V of 1915. In particular, in Items 97 and 98, MacMahon shows that the permutations which can be divided into two decreasing subsequences (i.e., the 123-avoiding permutations) are counted by the Catalan numbers.

Another early landmark result in the field is the Erdős–Szekeres theorem; in permutation pattern language, the theorem states that for any positive integers a and b every permutation of length at least ab+1 must contain either the pattern 1,2,3,...,a+1 or the pattern b+1,b,...,2,1.

Computer science origins

The study of permutation patterns began in earnest with Donald Knuth's consideration of stack-sorting in (1968). Knuth showed that the permutation π can be sorted by a stack if and only if π avoids 231, and that these permutations are enumerated by the Catalan numbers (1968, Section 2.2.1, Exercises 4 and 5). Knuth also raised questions about sorting with deques. In particular, (1968, Section 2.2.1, Exercise 13), which asks how many permutation of n elements are obtainable with the use of a deque, remains an open question (it is rated M49 in the first printing, and M48 in the second). Shortly thereafter, Robert Tarjan investigated sorting networks in (1972), while Vaughan Pratt showed in (1973) that the permutation π can be sorted by a deque if and only if for all k, π avoids 5,2,7,4,...,4k+11,4k−2,3,4k,1, and 5,2,7,4,...,4k+3,4k,1,4k+2,3, and every permutation that can be obtained from either of these by interchanging the last two elements or the 1 and the 2. Because this collection of permutations is infinite (in fact, it is the first published example of an infinite antichain of permutations), it is not immediately clear how long it takes to decide if a permutation can be sorted by a deque. Rosenstiehl & Tarjan (1984) later presented a linear (in the length of π) time algorithm which determines if π can be sorted by a deque.

In his paper, Pratt remarked that this permutation pattern order “seems to be the only partial order on permutation that arises in a simple and natural way” and concludes by noting that “from an abstract point of view”, the permutation pattern order “is even more interesting than the networks we were characterizing”.

Enumerative origins

Main article: Enumerations of specific permutation classes

Another major influence on the early development of the study of permutation patterns came from enumerative combinatorics, and focused on finding formulas for the number of permutations which avoid a fixed (and typically short) permutation. Let Avn(β) denote the set of permutations of length n which avoid β. As already noted, MacMahon and Knuth showed that |Avn(123)| = |Avn(231)| = Cn, the nth Catalan number. Thus these two patterns are equally difficult to avoid. Simion & Schmidt (1985) was the first paper to focus solely on enumeration. Among other results, Simion and Schmidt counted even and odd permutations avoiding a pattern of length three, counted permutations avoiding two patterns of length three, and gave the first bijective proof that 123- and 231-avoiding permutations are equinumerous. Since their paper, many other bijections have been given, see Claesson & Kitaev (2008) for a survey.

In general, if |Avn(β)| = |Avn(σ)| for all n, then β and σ are said to be Wilf-equivalent. Many Wilf-equivalences stem from the trivial fact that |Avn(β)| = |Avn(β−1)| = |Avn(βrev)| for all n, where β-1 denotes the inverse of β and βrev denotes the reverse of β. (These two operations generate the Dihedral group D8 with a natural action on permutation matrices.) However, there are also numerous examples of nontrivial Wilf-equivalences:

From these two Wilf-equivalences and the inverse and reverse symmetries, it follows that there are three different sequences |Avn(β)| where β is of length four:

β sequence enumerating Avn(β) OEIS reference exact enumeration reference
 1342  1, 2, 6, 23, 103, 512, 2740, 15485, 91245, 555662, ... A022558 Bóna (1997)
 1234  1, 2, 6, 23, 103, 513, 2761, 15767, 94359, 586590, ... A005802 Gessel (1990)
 1324  1, 2, 6, 23, 103, 513, 2762, 15793, 94776, 591950, ... A061552 unknown

In the late 1980s, Richard P. Stanley and Herbert Wilf conjectured that for every permutation β, there is some constant K such that |Avn(β)| < Kn. This was known as the Stanley–Wilf conjecture until it was proved in (2004) by Adam Marcus and Gábor Tardos.

Closed classes

A closed class, also known as a pattern class, permutation class, or simply class of permutations is a downset in the permutation pattern order. Every class can be defined by the minimal permutations which do not lie inside it, its basis. Thus the basis for the stack-sortable permutations is {231}, while the basis for the deque-sortable permutations is infinite. The generating function for a class is Σ x|π| where the sum is taken over all permutations π in the class.

Given a class of permutations, there are numerous questions that one may seek to answer, such as:

General techniques to answer these questions are few and far between.

Packing densities

The permutation π is said to be β-optimal if no permutation of the same length as π has more copies of β. In his address to the SIAM meeting on Discrete Mathematics in 1992, Wilf defined the packing density of the permutation β of length k as

\lim_{n\rightarrow\infty} \frac{\text{number of copies of }\sigma\text{ in a }\beta\text{-optimal permutation of length }n}{\displaystyle{n\choose k}}.

An unpublished argument of Fred Galvin shows that the quantity inside this limit is decreasing for n ≥ k, and so the limit exists. When σ is monotone, its packing density is clearly 1, and packing densities are invariant under the group of symmetries generated by inverse and reverse, so for permutations of length three, there is only one nontrivial packing density. Walter Stromquist (unpublished) settled this case by showing that the packing density of 132 is 2√3 - 3, approximately 0.46410.

For permutations β of length four, there are (due to symmetries) seven cases to consider:

β packing density reference
 1234  1 trivial
 1432  root of x3 - 12x2 + 156x - 64 ≅ 0.42357 Price (1997)
 2143  ⅜ = 0.375 Price (1997)
 1243  ⅜ = 0.375 Albert et al. (2002)
 1324  conjectured to be ≅ 0.244
 1342  conjectured to be ≅ 0.19658
 2413  conjectured to be ≅ 0.10474

For the three unknown permutations, there are bounds and conjectures. Price (1997) used an approximation algorithm which suggests that the packing density of 1324 is around 0.244. Birjan Batkeyev (unpublished) constructed a family of permutations showing that the packing density of 1342 is at least the product of the packing densities of 132 and 1432, ≅ 0.19658. This is conjectured to be the precise packing density of 1342. Recently, Presutti & Stromquist (2010) have provided a lower bound on the packing density of 2413. This lower bound, which can be expressed in terms of an integral, is approximately 0.10474, and conjectured to be the true packing density.

Generalizations

There are several ways in which this notion of permutation patterns may be generalized. For example, a vincular pattern is a permutation containing dashes indicating the entries that need not occur consecutively (in the normal pattern definition, no entries need to occur consecutively). For example, the permutation 314265 has two copies of the dashed pattern 2-31-4, given by the entries 3426 and 3425. For a dashed pattern β and any permutation π, we write β(π) for the number of copies of β in π. Thus the number of inversions in π is 2-1(π), while the number of descents is 21(π). Going further, the number of valleys in π is 213(π) + 312(π), while the number of peaks is 231(π) + 132(π). These patterns were introduced by Babson & Steingrímsson (2000), who showed that almost all known Mahonian statistics could be expressed in terms of vincular permutations. For example, the Major index of π is equal to 1-32(π) + 2-31(π) + 3-21(π) + 21(π).

Another generalization is that of a barred pattern, in which some of the entries are barred. For π to avoid the barred pattern β means that every set of entries of π which form a copy of the nonbarred entries of β can be extended to form a copy of all entries of β. West (1993) introduced these types of patterns in his study of permutations which could be sorted by passing them twice through a stack. (Note that West's definition of sorting twice through a stack is not the same as sorting with two stacks in series.) Another example of barred patterns occurs in the work of Bousquet-Mélou & Butler (2007), who showed that the Schubert variety corresponding to π is locally factorial if and only if π avoids 1324 and 21354.

References

External links